Create a Queue by only using stacks!

A very popular algorithm related question is asked during many programming interviews – “Write a program to create a queue by only using stack”. This question usually leaves even an experienced programmer confused about how to approach this question. The solution, however, is quite simple.

First, let’s understand the very basics of stacks and queues:

Stack: A stack is a data structure, which follows the policy of LIFO (Last In, First Out). Imagine a stack of plates placed on top of each other. If you were to retrieve a plate, you will take out the topmost plate first, right? This is exactly what happens in a stack. The element, which was inserted in the end, is retrieved first, while the element which was inserted first is retrieved last. From an implementation perspective, this data structure allows the following operations:

1. push(element) – This method allows to add an element on top of stack.
2. pop() – This element removes the top element from the stack.
3. peek() – This element views the top element of the stack, but does not remove it.
4. empty() – Checks if stack is empty. If stack has no elements, this should return true.

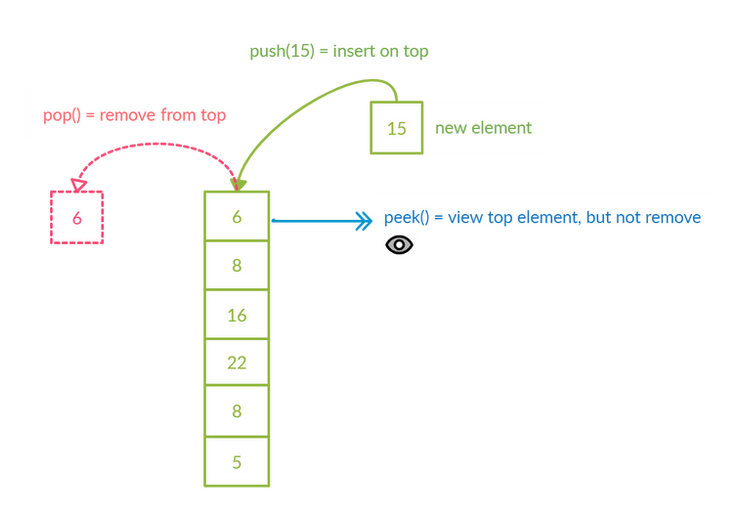
The above diagram represent a stack shown in the form of elements on top of each other. The element “5” was the first to come (and hence at the bottom). The element “6” was added LAST. Since the elements can only be removed from top, “6” will be the first to go. Therefore, it represents Last-In-First-Out (LIFO) policy.

Queue: A queue is a data structure, which follows the policy of FIFO (First In First Out). Imagine that you are in a queue for buying tickets for a popular movie. A person who came first, will buy the ticket first and will be out of the queue first. However, if a new person is joining the queue, he must go to the end of the queue and wait for his turn. Speaking in programmatic terms, in queue, we can insert elements in the end (or tail), and remove them from the beginning (head) of the queue. There are different types of queues which allow more operations than the ones stated above, but; for the sake of simplicity, we will just go ahead with the basic queue. Operations of a queue include:

1. offer(element) – adds an element to the tail of the list
2. poll() – removes the element at the head of the list
3. peek() – views the element at the head of the list
4. isEmpty() – checks if there are no elements in the queue

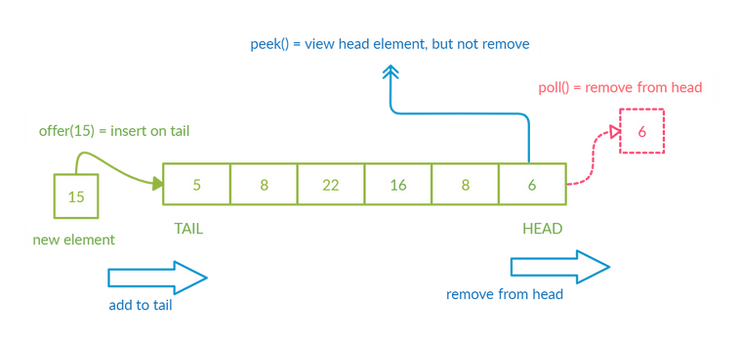
The above diagram represents a queue, we see that elements are added to the tail and removed from the head. Which means, the element “6” was the FIRST to arrive and “5” was the last to arrive. Since the elements can only be removed from the head, therefore “6” which came FIRST, will be the FIRST to go out. Therefore, it follows the policy of First-In-First-Out (FIFO).

---

The Logic of using stacks to form a Queue

In order to create a data structure behave like a queue, we will have to make use of two stacks., each of which has its own purpose. Let’s call them pushStack and popStack.

1. pushStack: Any new elements coming in, will be inserted into this stack. Therefore, for the offer(e) method of our queue, we will actually do a push(e) into the pushStack.
2. popStack: Any elements which are being removed or peeked from the queue, will be popped/peeked from this stack. Therefore, the poll() method of our queue will internally pop() from this stack. Also, the peek() method of the queue, will internally call peek() of this stack.

Now, the question arises, that we are inserting the elements in one stack, but removing from another. How will this popStack have elements inside it? Also – why are we using two stacks?

In the beginning, the popStack will be empty. Let’s say that the elements are being inserted into the pushStack. The moment poll() operation is called, it will internally call the pop() method of the popStack. But, popStack does not have any elements inside it. In this case, we will pop all the elements of the pushStack one-by-one and insert then in the popStack.

Doing this, will reverse the order of the inserted elements. On reversal of inserted elements, the bottom-most element of the stack now becomes the top-most element of the popStack. i.e. the element which was “inserted” first, can now be removed “first”, which is the whole concept of a queue.

It will be a bit more clear by the below graphical representation

Step#1: In the beginning, both stacks are empty

Step#2: Elements added to the queue

Therefore, the elements are inserted from the top. “5” is inserted first and goes at the bottom. “8” is inserted next, so its in the middle. “10” is inserted at last, and hence is on the top.

Step#3: Poll (remove) the element from the queue

When we poll() an element from a queue, it is removed from the head of the list. Right now, we have a stack in which, the “first-in” element (i.e. “5”) is at the bottom. According to the queue policy, the element coming-in first, should be the first to go out. However, stack only allows removal of the element from the top (in this case “10”). To counter this problem, we start popping all the elements one-by-one from the pushStack and then insert them into popStack.

As we can see, the order of the elements is reversed. In this context, the elements are now arranged in the form of first-in-first-out. “5” was first to come, and is on the top. “8” was second, and “10” was third. Therefore, if the poll() method of the queue is called and there are no elements in the popStack, we move all the elements of the pushStack to popStack. When this is done, then we can pop the topmost element of the popStack. In this case “5” will be popped. If the poll()method of queue is called again, then popStack still has some elements, and they can be popped. We can repeatedly call the pop() method of popStack until it is empty. The moment it becomes empty, we move the elements from the pushStack to popStack and again repeat the operation.

Step#4: Subsequent Insertion

In the above step, let’s assume “5” was polled from the queue (popped from popStack). At this moment, popStack still has some items, while pushStack is empty (we moved all the elements in previous step)

Let’s say that immediately after poll() method, offer(e) was called to insert some elements. In this case, we simply push the element into pushStack.

We can continue to follow steps 1 through 4 by following these basic principles

1. Always add elements to the pushStack.
2. Always remove elements from the popStack.
3. If popStack is empty && pushStack is empty | It means that the queue is empty
4. If popStack is empty && pushStack is not empty | move the elements to the popStack

This way, we can ensure that our data structure behaves like a queue.

Now, that we know what we have to implement, let’s see the code implementation.

---

Code Implementation

import java.util.Stack;
public class Queue<T> {
    private Stack<T> pushStack;
    private Stack<T> popStack;

    public Queue() {
        this.pushStack = new Stack<>();
        this.popStack = new Stack<>();
    }

    public void offer(T element) {
        //Always add to the pushStack.
        pushStack.push(element);
    }

    public T poll() {
        T element = peek();
        if (element != null) {
            //if element is not null, 
            //then popStack has some values and we pop it.
            popStack.pop();
        }
        return element;
    }

    public T peek() {
        if (popStack.size() == 0 && pushStack.size() > 0) {
            //if popstack is empty, but pushStack has data, 
            //then transfer the data to popStack
            while (pushStack.size() != 0) {
                //POP from pushStack and 
                //PUSH that element in the popStack
                popStack.push(pushStack.pop());
            }
        }
        //If popStack still has no values, then return null, 
        //otherwise, peek and display
        return popStack.size() > 0 ? popStack.peek() : null;
    }

}

Runtime Complexity Analysis

Complexity of offer(e): It is a straightforward addition to the top of a stack. Therefore, it happens in O(1) time (constant time).

Complexity of poll()/peek() : If we have some elements in the popStack, and we are removing an element from the top, it is constant time. However, when popStack is empty, we have to pop() all the elements from the pushStack in O(n) time. This operation happens once in a while when the popStack is empty, therefore, we can say that the complexity is O(1) in amortized time.

Questions? Comments? Feel free to put-in your thoughts in the comments section : )